7 TUNNUSLUVUT

Frekvenssit ja diagrammit eivät aina riitä tilastojen havainnollistamiseksi. Tämän vuoksi havaintoaineistoa voidaan kuvata erilaisilla tunnusluvuilla.

Keskiarvo ilmaisee muuttujan arvojen keskimääräisen suuruuden. Se lasketaan jakamalla muuttujan arvojen summa arvojen lukumäärällä

Esimerkki 7.1. Kokkiopiskelijan päästötodistuksessa oli äidinkieli 3, englanti 4, matematiikka 5, tietotekniikka 5 ja liikunta 1. Mikä oli näiden aineiden keskiarvo?

= (3 + 4 + 5 + 5 + 1) / 5 = 3,6

Luokitellussa aineistossa käytetään keskiarvonlaskemisessa luokkakeskuksia.

Esimerkki 7.2. Esimerkin 5.1 oppilaiden pituuksien keskiarvo lasketaan kertomalla kunkin luokan luokkakeskus sen frekvenssillä ja jakamalla frekvenssien summalla:

= (5·155,5 + 7·165,5 + 7·175,5 + 3·185,5)/22 = 169,1 (cm).

Mediaani ilmaisee keskimmäisen muuttujan arvon. Aineisto on laitettava suuruusjärjestykseen ennen mediaanin määrittämistä, joten muuttujan on oltava vähintään järjestysasteikollinen. Jos muuttujan arvoja on parillinen määrä, käytetään mediaanina kahden keskimmäisen muuttujan arvon keskiarvoa.

Esimerkki 7.3. Esimerkin 7.1 kokkiopiskelijan arvosanojen 1,3, 4, 5, 5 keskimmäinen arvo eli mediaani Md = 4.

Luokitellussa aineistossa mediaani on sen luokan luokkakeskus, joka jakaa muuttujan arvot kahteen yhtä suureen osaan.

Esimerkki 7.4. Esimerkin 5.1 oppilaiden pituudet olivat

Koska muuttujan arvoja on yhteensä 22 (ts. n = 22), keskimmäiset muuttujan arvot ovat yhdestoista ja kahdestoista arvo. Nämä muuttujan arvot ovat mediaaniluokassa 161-170 cm, joten mediaani Md = 165,5 cm.

Tyyppiarvo eli moodi (Mo) on muuttujan yleisin arvo. Moodin frekvenssi on siis suurin.

Esimerkki 7.5. Opiskelijan todistuksen arvosanat jakautuivat seuraavasti:

Eniten on arvosanoja 3 (6 kpl), joten se on moodi: Mo = 3.

Hajontaluvut kertovat, kuinka lähellä keskiarvoa muuttujan arvot ovat. Kahdella muuttujalla voi olla sama keskiluku (esimerkiksi keskiarvo), mutta niiden hajonta voi olla täysin erilainen. Hajontalukuja käytetään erityisesti silloin, kun halutaan vertailla kahta jakaumaa.

Yksinkertaisin hajontaluku on vaihteluvälin pituus, R. Se on muuttujan suurimman ja pienimmän arvon erotus. Luokitetulla aineistolla vaihteluväli lasketaan ylimmän luokan ylärajan ja alimman luokan alarajan erotuksena.

Tarkemmin muuttujan arvon hajontaa kuvaa keskihajonta. Se on havaintojen keskimääräinen poikkeama keskiarvosta. Keskihajontaa laskettaessa otetaan huomioon jokainen havainto ja sen erotus havaintojen keskiarvosta. Mitä lähempänä keskiarvoa ja toisiaan havaintoarvot ovat, sitä pienempi keskihajonta on.

Otoksen keskihajonnan kaava on

, missä

 

 x_i:t ovat havaintoarvoja

on keskiarvo

n on havaintojen lukumäärä.

Useimmissa laskimissa on näppäimet sekä otoksen (jaetaan arvolla n-1) että perusjoukon (jaetaan arvolla n = N) keskihajonnan laskemiseksi. Excelissä funktio keskihajonta laskee hajonnan otoksen perusteella ja funktio keskihajontap perusjoukon hajonnan.

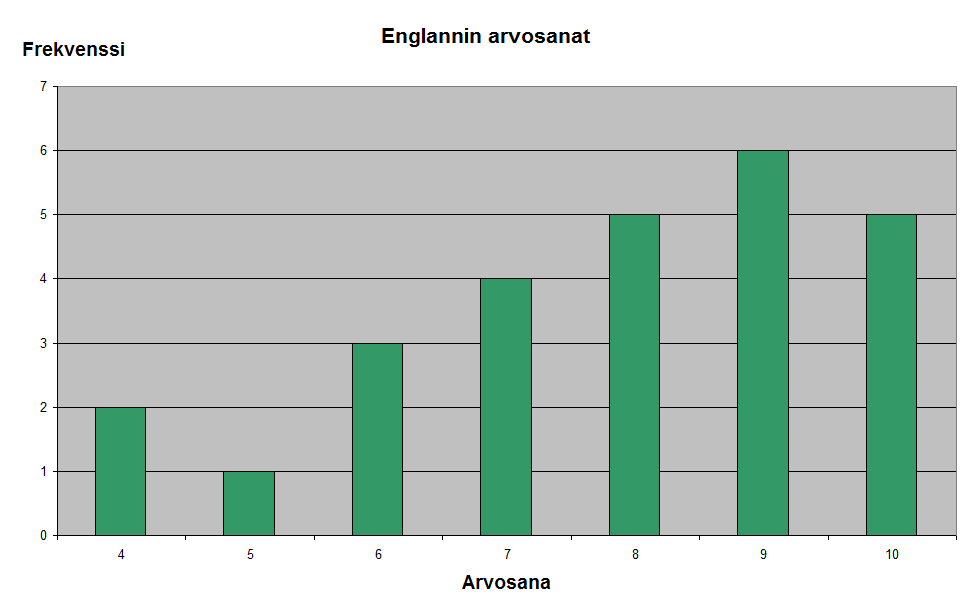
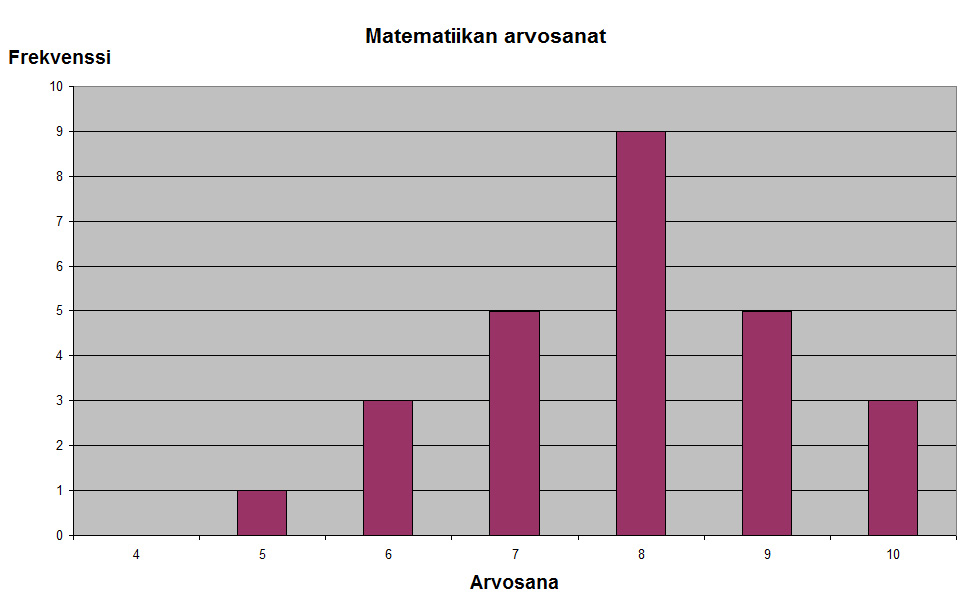
Esimerkki 7.6. Erään luokan oppilaiden arvosanat englannissa ja matematiikassa jakautuivat seuraavasti:

Englannin arvosanojen vaihteluvälin pituus R_englanti  = 10 - 4 = 6 ja matematiikan arvosanojen vaihteluvälin pituus R_matematiikka = 10 - 5 = 5.

Excelillä lasketut keskihajonnat ovat s_englanti = 1,8 ja s_matematiikka = 1,3.

Vaikka keskiluvut eivät juuri poikkea englannin ja matematiikan arvosanojen jakaumien välillä, jakaumien hajontaluvuista huomaa, että arvosanat matematiikassa ovat jakautuneet lähemmäs jakauman keskiarvoa kuin englannissa.