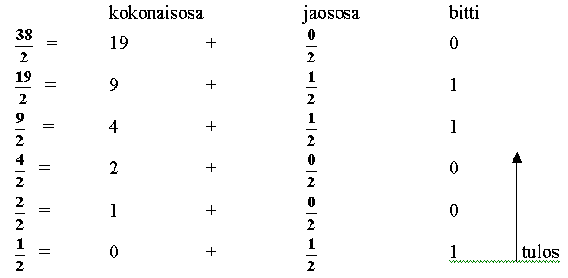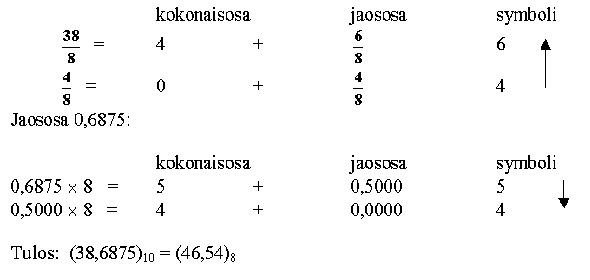4. Muunnoksia lukujärjestelmien välillä

 

4.1  Desimaaliluvusta toiseen järjestelmään

 

Desimaaliluvun muuntaminen binääriseksi
 

Desimaaliluvun muuntaminen toiseen järjestelmään edellyttää kokonaisosan ja jaososan käsittelyä erikseen eri algoritmeilla.

 

Esim. Muunnetaan luku 38,6875 binääriseksi.

 

Muunnetaan kokonaisosa 38 ensin. Lukua jaetaan toistuvasti kantaluvulla 2. Jaososa kertoo bitin.

 

 

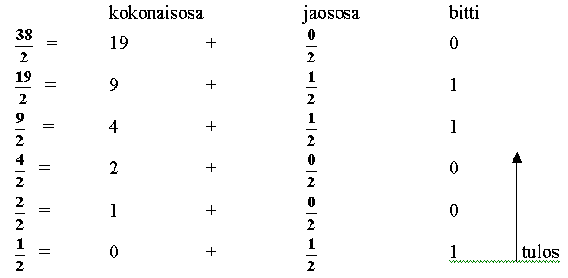
Jakamista jatketaan, kunnes kokonaisosa on nolla.

Tulos muodostuu jakojäännöksistä ja ne luetaan käänteisessä järjestyksessä.

Tulos: (38)10 = (100110)2 

 

Seuraavaksi muunnetaan jaososa 0,6875. Jaososaa kerrotaan kantaluvulla 2. Kokonaisosa kertoo bitin.

 

Tämä algoritmi päättyi kun jaososa on nolla. Usein myös jaososa on päättymätön. Tulos luetaan syntyvässä järjestyksessä.

Tulos: (0,6875)10 = (1011)2 

 

Eli (38,6875)10 = (100110,1011)2 

 

Desimaaliluvun muuntaminen oktaali- ja heksadesimaalijärjestelmään

 

Desimaaliluvun muuntaminen tapahtuu samoin kuin edellä. Jakajana tai kertojana on kantaluku 8 tai 16.

 

Esim. Muunnetaan luku 38,6875 oktaaliluvuksi.

 

Kokonaisosa 38:

 

 

Oppimistehtävä 7.

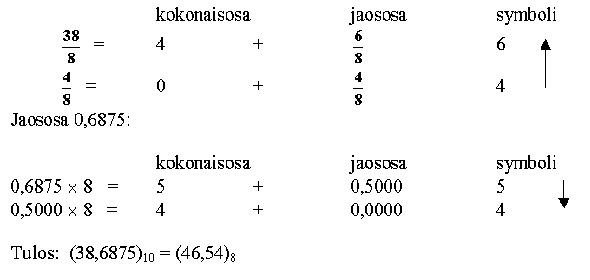
Tehtävänäsi on soveltaa edellä esitettyä tapaa heksadesimaalijärjestelmään. Muunna kymmenjärjestelmän luku 1056,024 heksadesimaalijärjestelmän luvuksi. Muista, että symbolit ovat kirjaimia A-F luvuilla 10-15.

 

 

 

4.2 Muunnokset 2-, 8- ja 16-järjestelmien välillä

Kantaluvut 8 ja 16 ovat kakkosen kokonaispotensseja. Oktaali- ja heksadesimaalijärjestelmän käyttä perustuu siihen. Muunnokset binäärijärjestelmän kanssa käy vaivattomasti. Heksadesimaalinumerot voidaan esittää neljällä bitillä ja oktaalinumerot kolmella.

 

 

Muunnoksessa bitit ryhmitellään kolmen tai neljän bitin ryhmiin alkaen aina desimaalipilkusta oikealle ja vasemmalle. Loppuun ja alkuun täydennetään tarvittaessa nollia.

 

 

Esim. Muunnetaan heksadesimaaliluku (B77C,0A)16 oktaaliluvuksi.

 

1.   Ilmoitetaan jokainen luku binäärilukuna. Huom! neljällä bitillä. Voit käyttää Oppimistehtävässä 4 tekemääsi taulukkoa apuna.

 

(B77C,0A)16 = (1011 0111 0111 1100, 0000 1010)2

 

 

2.   Muutetaan nyt binääriluku oktaaliluvuksi. Ryhmitellään kolmen bitin ryhmiin. Aloitetaan desimaalipilkusta. Alkuun ja loppuun lisätään tarvittavat nollat, että saadaan kolmen bitin ryhmä ”täyteen”.

 

(001 011 011 101 111 100, 000 010 100)2 

 

 

3.     Seuraavaksi katsotaan mitä oktaalilukua kukin kolmen bitin ryhmä vastaa. Voit käyttää taas taulukkoa apuna.

 

(1 3 3 5 7 4, 0 2 4)8  

 

Eli (B77C,0A)16 = (133574,024)8  

 

 

Oppimistehtävä 8.

Tehtävänäsi on muuntaa oktaaliluku (70664,022)8 heksadesimaaliluvuksi. Muuntaminen tapahtuu samoin kuin yllä. Muista, että kun esität oktaaliluvun binäärisenä, luvut ilmoitetaan kolmella bitillä.