2.   Lukujärjestelmät

2.1 Kymmenjärjestelmä

Lukujärjestelmämme kantalukuna on luku 10. Lienee sormien lukumäärällä on tämän kanssa jotain tekemistä, kun tähän kantalukuun on aikojen kuluessa päädytty...

Olemme tottuneet käyttämään ns. paikkamerkintää, kun ilmoitamme lukumäärää, eli jokainen ”paikka” kertoo luvusta tietyn asian.

 

 Esim.         luku           1789,56

Luku sisältää
 

- yhden kappaleen tuhansia	1x1000
- seitsemän kappaletta satoja	7x100
- kahdeksan kappaletta kymmeniä	8x10
- yhdeksän kappaletta ykkösiä	9x1
- viisi kappaletta kymmenesosia	5x0,1
- kuusi kappaletta sadasosia	6x0,01

Eli  1x1000 + 7x100 + 8x10 + 9x1 + 5x0,1 + 6x0,01 = 1789,56

 

Ilmoitetaan nyt luvut käyttäen kantalukua 10 ja potenssia:

 

1x10³ + 7x10² + 8x10¹ + 9x10⁰ + 5x10^-1 + 6x10^-2 = 1789,56

 

 

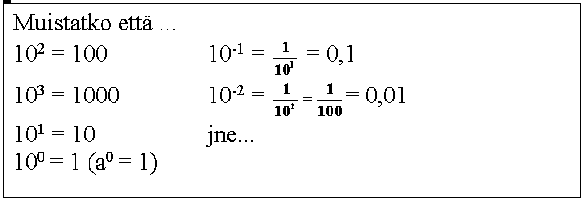
Huomaa, että desimaalipilkun vasemmalla puolella on nollannen potenssin paikka.

 

Kymmenjärjestelmässä eli desimaalijärjestelmässä on kantaluvun verran symboleita: 0, 1, 2, 3, 4, 5, 6, 7, 8 ja 9. Symbolit ovat piirrosmerkkejä, mutta ne voisivat olla myös muitakin merkkejä, kuten jopa ääni- tai valomerkkejä.

 

 

 

 

 

 

 

 

2.2   Binäärijärjestelmä

Binääri- eli kaksijärjestelmän numerosymboleina eli bitteinä (binary digit) olemme tottuneet käyttämään symboleita 0 ja 1.

 

Binäärijärjestelmän kantalukuna siis 2.

 

Binäärijärjestelmässä käytetään vastaavanlaista paikkamerkintää kuin desimaalijärjestelmässä. Erona vain se, että kantaluku on 2 ja symboleina 0 ja 1.

Oppimistehtävä 1.

a) Selvitä edellä mainittujen ohjeiden perusteella, miten binääriluku 11011,11 ilmoitetaan käyttäen kantalukua kaksi.

 

Kymmenjärjestelmässä binääriluvun tulisi olla 27,75.

 

Ettei eri lukujärjestelmien luvut mene sekaisin, voi kantaluvun ilmoittaa alaindeksissä seuraavasti:

                                   (11011,11)₂ = (27,75)₁₀

b) Ilmoita myös binääriluvut (111011,001)₂,  (1110)₂ ja (1011)₂ kymmenjärjestelmässä.

 

Kun kantaluku on pieni ja symboleita vain kaksi, tulee lukujen esityksistä pitkiä numerojonoja. Se onkin binäärijärjestelmän suurin haittapuoli. Sen takia käytetään myös oktaali- ja heksadesimaalijärjestelmää, jolloin esityksiä voidaan esittää lyhyemmässä muodossa.

2.3  Oktaalijärjestelmä

Oppimistehtävä 2.

Oktaalijärjestemässä kantaluku on 8 ja symboleja 8 eli 0, 1, 2, 3, 4, 5, 6 ja 7.

 

Ilmoita seuraavat oktaalijärjestelmän luvut kymmenjärjestelmässä. Hajota luvut käyttäen kantalukua 8.

a)     (1055,06)₈

 

b)    (456,2)₈    

2.4   Heksadesimaalijärjestelmä

Oppimistehtävä 3.

Heksadesimaalijärjestelmässä kantaluku on 16 ja symboleita 16. Vakiintuneeksi tavaksi on tullut ottaa käyttöön numerosymboleiden lisäksi kuusi ensimmäistä aakkosta: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E ja F. Ilmoita kymmenjärjestelmässä seuraavat heksadesimaaliluvut. Hajota luvut käyttäen kantalukua 16.

 

a)     (C1A,007)₁₆

 

b)    (FB1)₁₆

 

c)     (9A67,00A)₁₆ 

Oppimistehtävä 4.

Laadi taulukko missä desimaalijärjestelmän luvut 0-15 on esitetty kaikissa yllä mainituissa lukujärjestelmissä.

Oppimistehtävä 5.

Tehtävänäsi on keksiä oma lukujärjestelmäsi. Esittele se siten, että  vastaanottaja ei ymmärtäisi lukujärjestelmistä mitään. Valitse kantaluvuksi kymmentä pienempi luku. Esim. 3, 4, 5 tai 6. Symbolit voit keksiä itse. Esittele järjestelmäsi avulla ainakin luvut 0-20.