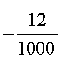
7.1 Desimaalijärjestelmä ja binäärijärjestelmä
1. Ilmoita käyttäen kantalukua 10
a) 78890,002 b) 0,2790 c)
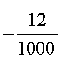
2. Kuinka paljon seuraavat binääriluvut ovat desimaalijärjestelmässä?
a) 11100,0101 b) 1110111 c) 1 d) 0010 e) 111
3. Laske
a) 110111 + 00111,1 b) 101111,1 + 110,011
4. Tarkista edelliset laskutoimitukset muuttamalla kymmenjärjestelmän luvuiksi ja vastaus binääriluvuksi.
5. Laske 101101 + 110101 + 001101 + 010001. Vastaus tulisi olla kymmenjärjestelmässä 128.
6. Mikä binääriluku pitäisi lukuun 111101 lisätä, jotta saadaan 1000100?
7.2 Muunnoksia ja laskutoimituksia
1. Muunna binääriluvuksi
a) (678,06)10 b) (10,9)10
2. Muunna desimaaliluvuksi
a) (100101,101)2 b) (30051,03)8 c) (1DBB,A)16
3. Muunna
a) (123,06)10 heksadesimaaliksi
b) (1001,09)10 oktaaliluvuksi
4. Esitä binääri- ja heksadesimaalilukuna oktaaliluvut
a) 66,707 b) 4332 c) 1234567
5. Esitä binääri- ja oktaalilukuna heksadesimaaliluvut
a) ABC b) 1234567 c) 007,C1A
6. Muunna
a) (EE101,0F)16 oktaaliluvuksi
b) (258,066)8 heksadesimaaliluvuksi
7. Laske
a) (45,75)10 + (111,011)2 vastaus binäärilukuna
b) (1111,1)2 + (10001)2 – (111,001)2 vastaus desimaalilukuna
c) (1010,001)2 x (1010,001)2
d) (007)8 + (FB1)16 + (C1A)16 + (00001)2 vastaus desimaalilukuna
8. Ratkaise x
a) (110011,01)2 + x = (1100111)2
b) (999)10 –x = (888)10
c) (ABC)16 + x = (87DF,5) 16 muuta luvut ensin desimaalijärjestelmään
1. Laske 10:n komplementti luvuille
a) 56669
b) 0,0965
c) 189,055
2. Laske 2:n komplementti luvuille
a) 1001111,1
b) 0,01101
c) 100011001100
3. Laske vähennyslaskut 10:n komplementilla
a) 2367 – 56672
b) 100000 – 1000000
4. Laske vähennyslaskut 2:n komplementilla
a) 1010111,1 – 1111111
b) 111 – 101
2.
Perusjoukko E sisältää 25 alkiota, joukko A 12
alkiota, A\B 7 alkiota ja ![]() 22
alkiota. Montako alkiota kuuluu joukkoon
22
alkiota. Montako alkiota kuuluu joukkoon
![]()
Havainnollista kuviota piirtämällä Venn-diagrammi.
3. Luettele joukon C = {1, 2, 3} kaikki osajoukot.
4. Olkoon E = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 5, 6, 7} ja B = {2, 6, 9}.
Määritä
a) –A b) A Ç B c) A – B
d) A Ç -B e) – (A Ç B)
f) Luettele ne B:n osajoukot, jotka sisältyvät joukkoon A.
5. Sievennä yksinkertaisempaan muotoon
a) A Ç (A È B) b) A È (A Ç B)
c) (A\B) Ç (B\A)
d) (A\B) È (B\A) È (A Ç B)
6. Pitävätkö seuraavat väitteet paikkaansa? Tee molemmista puolista ns. Venn-diagrammi ja vertaa syntyneitä alueita toisiinsa.
a) A È (B Ç C) = (A È B) Ç (A È C)
b) A Ç (B È C) = (A Ç B) È (A Ç C)
c) A – B = A Ç (-B)
7. Yksinkertaista seuraavia esityksiä
a) A Ç E e) A – (-A)
b) A È E f) A È Æ
c) E – A g) A - Æ
d) A – E
8. Mitä tarkoittavat merkinnät
A = {2k | k Î kokonaislukujen joukkoon Z}
A = {2k+1 | k Î kokonaislukujen joukkoon Z}?
9. Ilmoita joukko-opin operaatioita käyttäen seuraavat alueet:
a)
b)
c)
10. Piirrä Venn-diagrammi (kuten yllä) seuraavasta lauseesta:
![]()